Analyse complète du cas
L’analyse complète des cas (ACC), également appelée “suppression des cas par liste”, consiste à rejeter les observations lorsque des valeurs de l’une des variables sont manquantes. L’analyse complète des cas consiste à analyser littéralement uniquement les observations pour lesquelles il existe des informations dans toutes les variables de l’ensemble de données.
Quelles variables puis-je imputer avec l’ACC?
L’ACCpeut être appliquée à la fois aux variables catégorielles et numériques.
Hypothèses
L’ACCfonctionne bien lorsque les données sont complètement manquantes au hasard (MCAR). En fait, nous devrions utiliser l’ACCsi nous avons des raisons de croire que les données manquent au hasard, et non pas autrement. Lorsque les données sont MCAR, l’exclusion des observations comportant des informations manquantes revient essentiellement à exclure de manière aléatoire certaines observations de l’ensemble de données. Par conséquent, l’ensemble de données après l’ACC est une représentation équitable de l’ensemble de données original.
Avantages
- Facile à mettre en œuvre
- Aucune manipulation de données requise
- Préserve la distribution des variables (si les données sont MCAR, alors la distribution des variables de l’ensemble de données réduit doit correspondre à la distribution de l’ensemble de données original)
Inconvénients
- Elle peut exclure une grande partie de l’ensemble de données d’origine (si les données manquantes sont abondantes)
- Les observations exclues pourraient être instructives pour l’analyse (si les données ne sont pas manquantes au hasard)
- Le CCA créera un ensemble de données biaisées si les cas complets diffèrent des données originales (par exemple, lorsque les informations manquantes sont en fait MAR ou NMAR et ne manquent pas au hasard).
- Lors de l’utilisation de nos modèles en production, le modèle ne saura pas comment traiter les données manquantes
Quand utiliser la CCA
- Les données manquent complètement au hasard
- Pas plus de 5% de l’ensemble des données contiennent des données manquantes
En pratique, la CCA peut être une méthode acceptable lorsque la quantité d’informations manquantes est faible. Malheureusement, il n’existe pas de règle empirique pour déterminer si la quantité de données manquantes est faible ou négligeable. Toutefois, à titre indicatif, si la quantité totale de données manquantes est égale ou inférieure à ~5% de l’ensemble de données d’origine, la CCA est une option viable.
Dans de nombreux ensembles de données réelles, la quantité de données manquantes n’est jamais faible et, par conséquent, la CCA n’est généralement jamais une option.
La CCA et les modèles en production
Lorsque nous utilisons la CCA, nous supprimons toutes les observations qui contiennent des informations manquantes. Cependant, les données que nous voulons noter avec notre modèle peuvent en effet contenir des informations manquantes. Cela posera un problème lors de l’utilisation de notre modèle dans des systèmes réels, ou comme nous l’appelons, lors de la mise en place ou de la production de modèles : lorsqu’une observation contient des données manquantes, le modèle ne pourra pas la traiter.
Afin d’éviter ce problème, lors de la mise en production des modèles, nous devons faire l’une des deux choses suivantes : soit nous ne notons pas les observations comportant des données manquantes, soit nous remplaçons les valeurs manquantes par un autre nombre.
Dans mon jeu de données, je n’ai presque pas de données manquantes. Quelques part cela est rassurant car cela veut dire que ma base de données est propre. Par contre pour vous montrer un peu ce que l’on peut faire, je vais injecter des valeurs manquantes dans notre fichier d’étude.
Il existe des variables numériques et catégorielles pour lesquelles il manque des observations. Nous pouvons voir à partir des types de variables que certaines sont flottantes et d’autres sont des objets.
La première variable contient beaucoup d’informations manquantes. Nous ne pouvons donc pas utiliser la CCA si nous considérons cette variable, car la plupart des observations de l’ensemble de données seront rejetées.
Pour cette démonstration, je vais ignorer la variable nbPartants.1 et utiliser l’ACC dans le reste de l’ensemble de données.
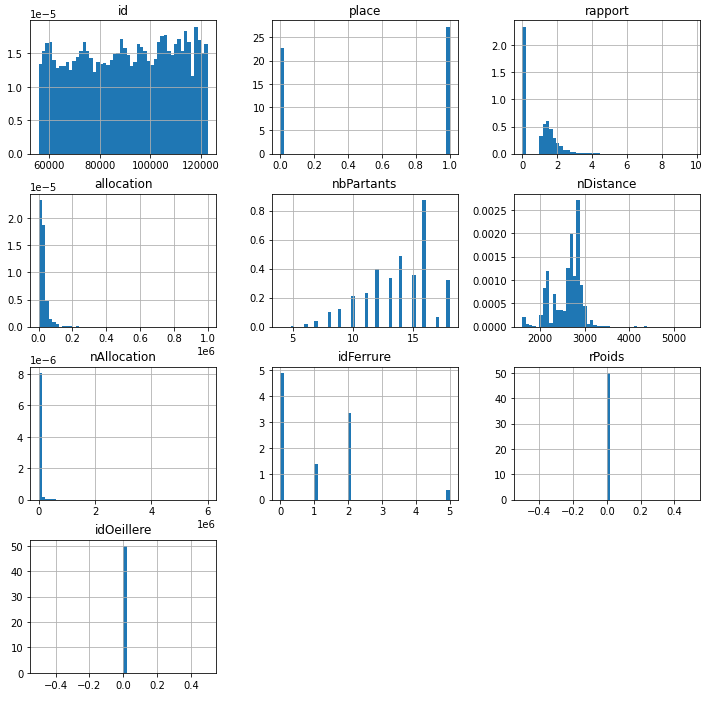
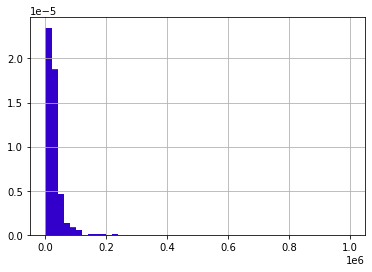
On ne distingue rien de spécial.La distribution semble identique.
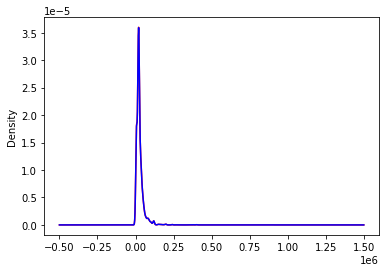
Comme nous pouvons le voir sur les graphiques ci-dessus, la distribution des variables numériques sélectionnées dans l’ensemble de données du cas original et du cas complet est très similaire, ce que nous attendons de la cca si les données manquent au hasard et seulement pour une petite partie des observations.
Dans les prochaines cellules, je vais étudier la distribution des variables catégorielles. Pour ce faire, j’évaluerai le pourcentage d’observations qui montrent chacune des catégories uniques, comme nous l’avons fait dans les sections 2 et 3 du cours.
Comme nous pouvons le voir d’après les résultats des cellules ci-dessus, la répartition des étiquettes dans chacune des catégories est très similaire dans l’ensemble de données original et complet du cas, ce qui, là encore, est ce à quoi on s’attend si les données sont complètement manquantes au hasard et si le pourcentage de données manquantes est faible.
Si vous voulez découvrir comment fonctionne la librairie pandas ou bien l’environnement Jupyter, n’hésitez pas à consulter les cours ci-dessous.
Je télécharge mon guide gratuit
Vous recevrez votre guide par email sans aucun engagement de votre part.