L’imputation consiste à remplacer les données manquantes par des estimations statistiques des valeurs manquantes. L’objectif de toute technique d’imputation est de produire un ensemble complet de données qui peut être utilisé pour former des modèles d’apprentissage automatique.
L’imputation moyenne / médiane consiste à remplacer toutes les occurrences de valeurs manquantes (NA) dans une variable par la moyenne (si la variable a une distribution gaussienne) ou la médiane (si la variable a une distribution asymétrique).
Notez ce qui suit :
- Si une variable est normalement distribuée, la moyenne, la médiane et le mode sont approximativement les mêmes. Par conséquent, le remplacement des valeurs manquantes par la moyenne et la médiane sont équivalents. Le remplacement des données manquantes par le mode n’est pas une pratique courante pour les variables numériques.
- Si la variable est faussée, la moyenne est biaisée par les valeurs à l’extrémité de la distribution. Par conséquent, la médiane est une meilleure représentation de la majorité des valeurs de la variable.
- Pour les variables discrètes exprimées sous la forme “int” (pour économiser de la mémoire), la moyenne peut ne pas être un nombre entier, et la variable entière sera donc recalculée sous la forme “float”. Afin d’éviter ce comportement, nous pouvons remplacer NA par la médiane à la place. La médiane sera inévitablement un entier / une valeur discrète également.
Quelles variables puis-je imputer avec l’imputation moyenne / médiane ?
La moyenne et la médiane ne peuvent être calculées que sur des variables numériques, ces méthodes ne conviennent donc qu’aux variables numériques continues et discrètes.
Hypothèses
- Les données sont complètement manquantes au hasard (MCAR)
- Les observations manquantes, ressemblent très probablement à la majorité des observations de la variable (alias, la moyenne / médiane)
Si les données manquent complètement au hasard, il est alors juste de supposer que les valeurs manquantes sont très probablement très proches de la valeur de la moyenne ou de la médiane de la distribution, car elles représentent l’observation la plus fréquente / moyenne.
Avantages
- Facile à mettre en œuvre
- Moyen rapide d’obtenir des ensembles de données complets
- Peut être intégré dans la production (lors du déploiement du modèle)
Limitations
- Distorsion de la distribution initiale des variables
- Distorsion de l’écart initial
- Distorsion de la covariance avec les autres variables de l’ensemble de données
Lorsque l’on remplace NA par la moyenne ou la médiane, la variance de la variable sera faussée si le nombre de NA est important par rapport au nombre total d’observations, ce qui entraîne une sous-estimation de la variance.
En outre, les estimations de la covariance et des corrélations avec d’autres variables de l’ensemble de données peuvent également être affectées. L’imputation de la moyenne / médiane peut modifier les corrélations intrinsèques puisque la valeur moyenne / médiane qui remplace maintenant les données manquantes ne préservera pas nécessairement la relation avec les autres variables.
Quand utiliser l’imputation moyenne / médiane ?
- Les données sont complètement manquantes au hasard
- Pas plus de 5 % de la variable contient des données manquantes
Bien qu’en théorie, les conditions ci-dessus devraient être remplies pour minimiser l’impact de cette technique d’imputation, en pratique, l’imputation moyenne / médiane est très couramment utilisée, même dans les cas où les données ne sont pas MCAR et où il y a beaucoup de valeurs manquantes. La raison en est la simplicité de la technique.
Note finale
Le remplacement de NA par la moyenne / médiane est largement utilisé dans la communauté des sciences des données et dans divers concours de sciences des données.
Généralement, l’imputation de la moyenne / médiane est effectuée en ajoutant une variable binaire “indicateur manquant” pour saisir les observations pour lesquelles les données sont manquantes , couvrant ainsi deux angles : si les données sont complètement manquantes au hasard, cela sera saisi par l’imputation de la moyenne / médiane, et si ce n’est pas le cas, cela sera saisi par la variable supplémentaire “indicateur manquant”. Ces deux méthodes sont extrêmement simples à mettre en œuvre et constituent donc un choix de premier ordre dans les concours de science des données.
La seule variable numérique pour laquelle il manque des données est iCote, avec environ 17 % d’observations manquantes.
Imputation
L’imputation doit être faite sur l’ensemble de formation, puis propagée à l’ensemble de test. Cela signifie que la moyenne / médiane à utiliser pour combler les valeurs manquantes à la fois dans le train et dans l’ensemble de test, doit être extraite de l’ensemble d’entrainement uniquement. Et ce, afin d’éviter tout surajustement.
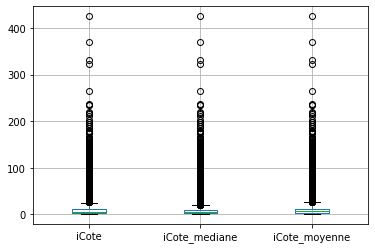
Comme prévu, la variance est sous-estimée, car maintenant de nombreuses valeurs sont identiques ==> soit la valeur moyenne, soit la valeur médiane.
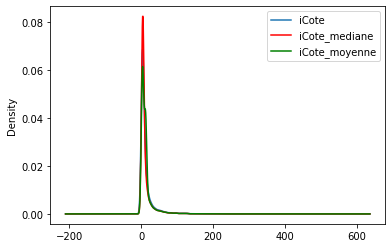
Comme mentionné ci-dessus, l’imputation moyenne / médiane déforme la distribution initiale de la variable iCote. La variable transformée présente plus de valeurs autour des valeurs moyennes / médianes.
Est-ce important ?
Cela dépend du modèle d’apprentissage machine que vous voulez construire. Les modèles linéaires supposent que les variables sont normalement distribuées. L’imputation de la moyenne / médiane peut déformer la distribution normale originale si le pourcentage de données manquantes est élevé. Par conséquent, la variable finale imputée ne sera plus normalement distribuée, ce qui peut affecter les performances du modèle linéaire.
Nous voyons en effet que la covariance entre la cote et l’allocation est modifiée après l’imputation moyenne / médiane.
Si vous voulez découvrir comment fonctionne la librairie pandas ou bien l’environnement Jupyter, n’hésitez pas à consulter les cours ci-dessous.
Je télécharge mon guide gratuit
Vous recevrez votre guide par email sans aucun engagement de votre part.