L’imputation consiste à remplacer les données manquantes par des estimations statistiques des valeurs manquantes. L’objectif de toute technique d’imputation est de produire un ensemble complet de données qui peut être utilisé pour former des modèles d’apprentissage automatique.
L’imputation de valeurs arbitraires consiste à remplacer toutes les occurrences de valeurs manquantes (NA) dans une variable par une valeur arbitraire. Les valeurs arbitraires généralement utilisées sont 0, 999, -999 (ou d’autres combinaisons de 9) ou -1 (si la distribution est positive).
Quelles variables puis-je imputer avec une valeur arbitraire ?
Les variables catégorielles et numériques peuvent être imputées par des valeurs arbitraires.
Pour les variables catégorielles, cela équivaut à remplacer toutes les instances de NA par une étiquette supplémentaire, ce qui est une pratique très courante ; je la traiterai donc séparément un peu plus tard.
Hypothèses
- Les données ne manquent pas au hasard.
Si c’est le cas, nous voulons signaler les valeurs manquantes avec une valeur différente (arbitraire), au lieu de remplacer ces occurrences par la moyenne ou la médiane, qui représentent la valeur la plus courante.
Avantages
- Facile à mettre en œuvre
- Moyen rapide d’obtenir des ensembles de données complets
- Peut être intégré dans la production (lors du déploiement du modèle)
- Saisit l’importance du “manque” s’il y en a un
Limitations
- Distorsion de la distribution de la variable d’origine
- Distorsion de l’écart initial
- Distorsion de la covariance avec les autres variables de l’ensemble de données
- Si la valeur arbitraire se trouve à la fin de la distribution, elle peut masquer ou créer des valeurs aberrantes
- Il faut veiller à ne pas choisir une valeur arbitraire trop semblable à la moyenne ou à la médiane (ou à toute autre valeur commune de la distribution de la variable)
Quand utiliser l’imputation de valeur arbitraire
Le remplacement des NA par des valeurs arbitraires doit être utilisé lorsqu’il y a des raisons de croire que les NA ne manquent pas au hasard. Dans de telles situations, nous ne voudrions pas remplacer par la médiane ou la moyenne, et donc faire en sorte que les NA ressemblent à la majorité de nos observations. Nous voulons plutôt signaler le fait que l’observation est manquante.
Cette approche est largement utilisée tant dans les organisations que dans les concours Kaggle. Elle consiste à remplacer la NA par une valeur arbitraire. N’importe laquelle de votre création, mais idéalement différente de la médiane/moyenne/mode, et non pas dans les valeurs normales de la variable.
Le problème consiste à décider de la valeur arbitraire à choisir…
Imputation importante
L’imputation doit être faite sur l’ensemble de formation, puis propagée à l’ensemble de test. Pour l’imputation de valeurs arbitraires, cela n’est pas si important, car nous avons choisi la valeur arbitrairement, cependant il est bon d’adhérer à cette pratique et de sélectionner la valeur arbitraire en regardant uniquement la distribution des variables dans l’ensemble de formation.
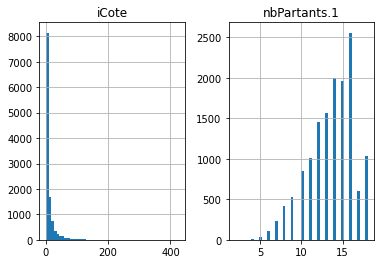
En fait, l’effet sur la variance sera également déterminé par l’ampleur de la valeur arbitraire choisie pour l’imputation, comparer 99 avec -1.
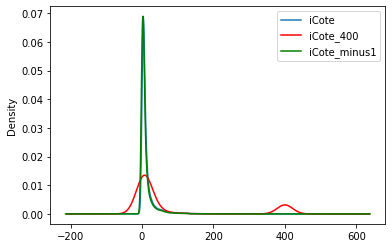
Comme mentionné ci-dessus, l’imputation déforme la distribution initiale de la variable iCote.
Est-ce important ?
Cela dépend du modèle d’apprentissage machine que vous voulez construire. Les modèles linéaires supposent que les variables sont normalement distribuées. L’imputation de la moyenne / médiane peut déformer la distribution normale originale si le pourcentage de données manquantes est élevé. Par conséquent, la variable finale imputée ne sera plus normalement distribuée, ce qui peut affecter les performances du modèle linéaire.
Si vous voulez découvrir comment fonctionne la librairie pandas ou bien l’environnement Jupyter, n’hésitez pas à consulter les cours ci-dessous.
Je télécharge mon guide gratuit
Vous recevrez votre guide par email sans aucun engagement de votre part.