Imputation la plus fréquente par catégorie | Imputation par mode
L’imputation consiste à remplacer les données manquantes par des estimations statistiques des valeurs manquantes. L’objectif de toute technique d’imputation est de produire un ensemble complet de données qui peut être utilisé pour former des modèles d’apprentissage automatique.
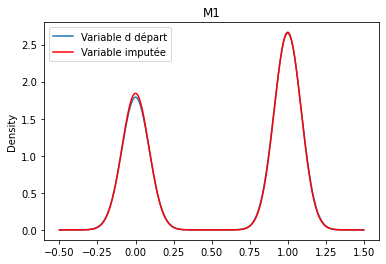
L’imputation par mode consiste à remplacer toutes les occurrences de valeurs manquantes (NA) au sein d’une variable par le mode, qui en d’autres termes se réfère à la valeur la plus fréquente ou à la catégorie la plus fréquente.
Quelles variables puis-je imputer avec l’imputation la plus fréquente / mode ?
Bien que le mode, ou la valeur la plus fréquente, puisse être calculé pour les variables numériques et catégorielles, en pratique, nous n’utilisons cette technique que pour les variables catégorielles. La raison en est que pour les variables numériques, la moyenne ou la médiane a tendance à mieux représenter la valeur moyenne de la population.
Hypothèses
- Les données sont complètement manquantes au hasard (MCAR)
- Les observations manquantes, ressemblent très probablement à la majorité des observations de la variable (aka, le mode)
Le raisonnement est que la valeur qui aurait dû être observée pour l’observation manquante est très probablement la valeur ou la catégorie la plus fréquente de la variable.
Avantages
- Facile à mettre en œuvre
- Moyen rapide d’obtenir des ensembles de données complets
- Peut être intégré dans la production (lors du déploiement du modèle)
Limitations
- Distorsion de la relation de l’étiquette la plus fréquente avec d’autres variables de l’ensemble de données
- Peut conduire à une surreprésentation du label le plus fréquent s’il y a un grand nombre de NA
Quand utiliser le mode / l’imputation par catégorie la plus fréquente ?
- Les données sont complètement manquantes au hasard
- Pas plus de 5 % de la variable contient des données manquantes
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# to split the datasets
from sklearn.model_selection import train_test_split
cols_to_use = ['M1', 'idHippodrome', 'place']
data = pd.read_csv('../exportfeature.csv',usecols=cols_to_use, sep=";",encoding='ANSI')
data.head()
# Imputation de valeur manquantes
# 0.03 % dans M1
data.loc[data.sample(frac=0.03).index, 'M1'] = np.nan
# 0.05 % dans Hippodrome
data.loc[data.sample(frac=0.06).index, 'idHippodrome'] = np.nan
# Vérification des valeurs manquantes
data.isnull().mean()place 0.000000
M1 0.029994
idHippodrome 0.059988
dtype: float64La variable M1 ne contient que quelques observations avec NA (2,9), c’est pourquoi le remplacement de ces observations par la valeur de la catégorie la plus fréquente est une bonne approche.
La variable idHippodrome ne contient que quelques observations avec NA (5,9), c’est pourquoi le remplacement de ces observations par la valeur de la catégorie la plus fréquente est une bonne approche.
Imputation importante
L’imputation doit être faite sur l’ensemble de formation, puis propagée à l’ensemble de test. Cela signifie que la catégorie la plus fréquente doit être sélectionnée dans l’ensemble d’entraînement et utilisée pour remplacer NA dans les ensembles d’entraînement et de test.
# Création du jeu d'entrainement et de test
X_train, X_test, y_train, y_test = train_test_split(
data,
data['place'],
test_size=0.3,
random_state=0)
X_train.shape, X_test.shape
((14352, 3), (6152, 3))M1
# % de valeurs absentes
X_train['M1'].isnull().mean()
0.029612597547380156
# examinons le nombre d'observations par catégorie dans M1
# nous avons utilisé cette ligne de code dans la section 3 sur les caractéristiques variables
# value_counts() compte le nombre de fois ou une étiquette est présnete
# dans la variable indiquée ci-dessous
X_train['M1'].value_counts().sort_values(ascending=False).plot.bar()
plt.xlabel('M1')
plt.ylabel('Nombre de fois')
# Etiquette la plus présente
X_train['M1'].mode()
0 1a
dtype: object
# traçons la distribution de la cible pour M1 qui :
# * montrent la catégorie la plus fréquente ou
# * ceux qui présentent des données manquantes
fig = plt.figure()
ax = fig.add_subplot(111)
X_train[X_train['M1']=='1a']['place'].plot(kind='kde', ax=ax)
X_train[X_train['M1'].isnull()]['place'].plot(kind='kde', ax=ax, color='red')
lines, labels = ax.get_legend_handles_labels()
labels = ['M1 avec 1a', 'M1 avec na']
ax.legend(lines, labels, loc='best')
plt.title('M1')
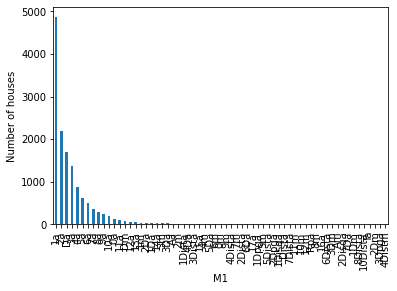
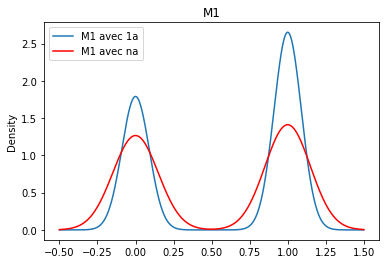
Le graphique ci-dessus indique que M1 pour lesquelles les données sont manquantes globalement se positionnent moins en placé.
# Je garde la distribution originale de place pour la plupart
# catégorie fréquente pour plus tard
# l'utilisation de tmp est commune pour nommer les variables temporaires
tmp = X_train[X_train['M1']=='1a']['place']
# Remplissons na à la fois le train et le test
# J'utilise la méthode fillna() des pandas
# avec l'argument inplace=True, j'indique aux pandas
# que je veux que les valeurs soient remplacées dans le même ensemble de données
X_train['M1'].fillna('1a', inplace=True)
X_test['M1'].fillna('1a', inplace=True)
# existe il encore des valeurs na
X_train['M1'].isnull().sum()
0 -> Non il n'en reste pas
# Evaluation de la distribution
X_train['M1'].value_counts().sort_values(ascending=False).plot.bar()
plt.xlabel('M1')
plt.ylabel('Nombre')
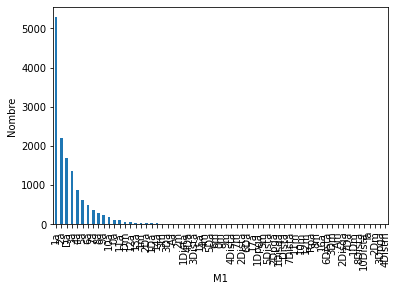
Nous pouvons voir que la catégorie 1a est désormais plus présente.
fig = plt.figure()
ax = fig.add_subplot(111)
tmp.plot(kind='kde', ax=ax)
X_train[X_train['M1'] == '1a']['place'].plot(
kind='kde', ax=ax, color='red')
lines, labels = ax.get_legend_handles_labels()
labels = ['Variable de départ', 'Variable imputée']
ax.legend(lines, labels, loc='best')
plt.title('M1')
Si vous voulez découvrir comment fonctionne la librairie pandas ou bien l’environnement Jupyter, n’hésitez pas à consulter les cours ci-dessous.
