Que faisons-nous de la variable après discrétisation ? Devons-nous les utiliser lcomme variable numérique ? ou devons-nous utiliser les intervalles comme variable catégorielle ?
La réponse est : vous pouvez faire l’un ou l’autre.
Si vous construisez des algorithmes basés sur des arbres de décision et que les résultats de la discrétisation sont des entiers (chaque entier se référant à un bac), alors vous pouvez les utiliser directement, car les arbres de décision détecteront des relations non linéaires entre la variable discrétisée et la cible.
Si vous construisez plutôt des modèles linéaires, les casiers n’auront pas nécessairement une relation linéaire avec la cible. Dans ce cas, il peut être utile d’améliorer les performances du modèle en traitant les casiers comme des catégories et en les soumettant à un codage à chaud, ou à des codages guidés par la cible comme le codage de la moyenne, le poids de la preuve ou le codage ordinal guidé par la cible.
Dans cette démo
Nous effectuerons une discrétisation à fréquence égale suivie d’un encodage guidé par la cible
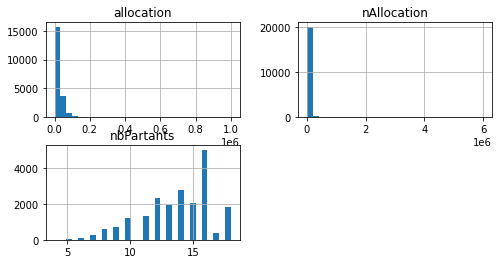
Discrétisation à fréquence égale avec Feature-Engine
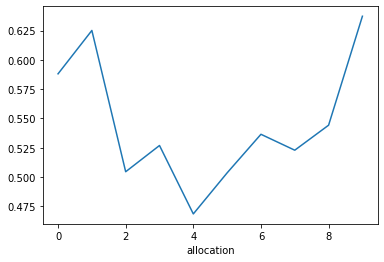
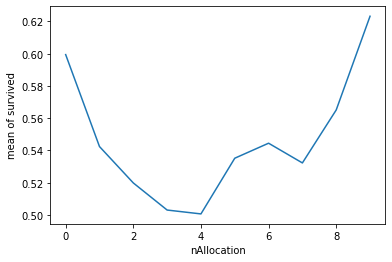
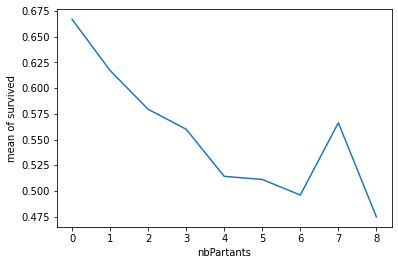
Avec le nombre de partants on peut voir que plus le nombre augmente plus la probabilité d’être à l’arrivée diminue. Par contre pour les allocations se sont les extrêmes qui augmentent les probabilité d’être à l’arrivée
Codage ordinal avec Feature-Engine
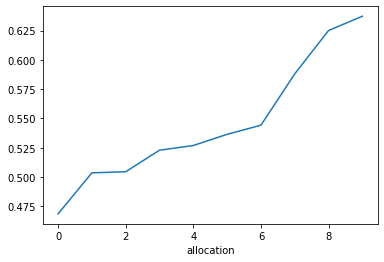
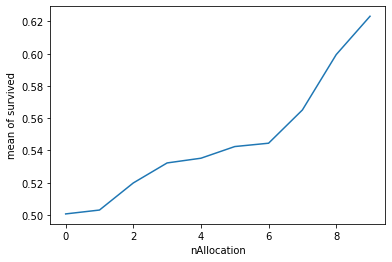
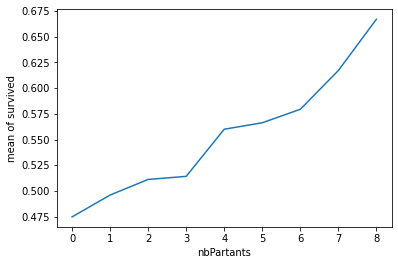
Nous avons maintenant obtenu une relation monotone entre les variables et la cible.
Si vous voulez découvrir comment fonctionne la librairie pandas ou bien l’environnement Jupyter, n’hésitez pas à consulter les cours ci-dessous.
Je télécharge mon guide gratuit
Vous recevrez votre guide par email sans aucun engagement de votre part.