La discrétisation est le processus qui consiste à transformer des variables continues en variables discrètes en créant un ensemble d’intervalles contigus qui couvrent la gamme des valeurs de la variable. La discrétisation est également appelée binning, où bin est un nom alternatif pour l’intervalle.
La discrétisation permet de traiter les valeurs aberrantes et peut améliorer la répartition des valeurs dans les variables biaisées
La discrétisation aide à traiter les valeurs aberrantes en plaçant ces valeurs dans les intervalles inférieurs ou supérieurs, avec les valeurs restantes plus anciennes de la distribution. Ainsi, ces observations aberrantes ne diffèrent plus du reste des valeurs à la queue de la distribution, car elles sont maintenant toutes ensemble dans le même intervalle/seau. De plus, en créant des cases ou des intervalles appropriés, la discrétisation peut aider à répartir les valeurs d’une variable biaisée sur un ensemble de cases ayant un nombre égal d’observations.
Approches de la discrétisation
Il existe plusieurs approches pour transformer les variables continues en variables discrètes. Les méthodes de discrétisation se divisent en deux catégories : supervisée et non supervisée. Les méthodes non supervisées n’utilisent aucune information, autre que la distribution des variables, pour créer les bacs contigus dans lesquels les valeurs seront placées. Les méthodes supervisées utilisent généralement des informations cibles pour créer les bacs ou les intervalles.
Méthodes de discrétisation non supervisées
- Discrétisation à largeur égale
- Discrétisation à fréquence égale
- La discrétisation de K-means
Méthodes de discrétisation supervisées
- Discrétion à l’aide d’arbres de décision
Dans ce notebook je décrirai la discrétisation à largeur égale.
Discrétisation de largeur égale
La discrétisation à largeur égale divise l’étendue des valeurs possibles en N cases de même largeur. La largeur est déterminée par l’étendue des valeurs de la variable et le nombre de cases que nous souhaitons utiliser pour diviser la variable :
largeur = (valeur maximale – valeur minimale) / N
où N est le nombre de bacs ou d’intervalles.
Par exemple, si les valeurs de la variable varient entre 0 et 100, nous créons 5 bacs comme ceci : largeur = (100-0) / 5 = 20. Les bacs sont donc 0-20, 20-40, 40-60, 80-100. Le premier et le dernier bac (0-20 et 80-100) peuvent être élargis pour tenir compte des valeurs aberrantes (c’est-à-dire que les valeurs inférieures à 0 ou supérieures à 100 seraient également placées dans ces bacs).
Il n’y a pas de règle empirique pour définir N, c’est-à-dire quelque chose à déterminer expérimentalement.
Dans cette démo
Nous apprendrons comment effectuer un binning de largeur égale avec
- Feature-engine
Super aucune données manquantes.
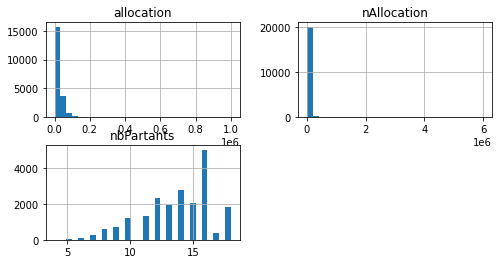
Discrétisation à largeur égale avec Feature-Engine
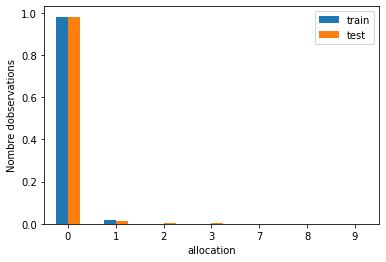
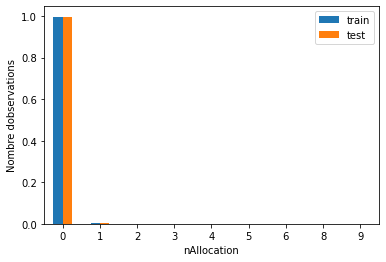
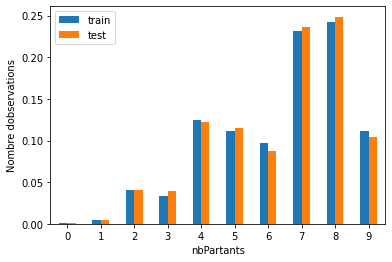
On voit bien que la discrétisation à largeur égale n’améliore pas l’écart de valeur. La variable originale allocation était biaisée, et la variable discrète l’est également.
Je télécharge mon guide gratuit
Vous recevrez votre guide par email sans aucun engagement de votre part.
Si vous voulez découvrir comment fonctionne la librairie pandas ou bien l’environnement Jupyter, n’hésitez pas à consulter les cours ci-dessous.
