Des étiquettes qui se produisent rarement
Les variables catégorielles sont celles dont les valeurs sont sélectionnées dans un groupe de catégories, également appelées labels. Différents labels apparaissent dans l’ensemble de données avec des fréquences différentes. Certaines catégories apparaissent beaucoup dans l’ensemble de données, tandis que d’autres catégories n’apparaissent que dans un nombre limité d’observations.
Par exemple, dans un ensemble de données contenant des informations sur les demandeurs de prêts dont l’une des variables est la “ville” où vit le demandeur, des villes comme “Paris” peuvent apparaître en grand nombre dans les données parce que Paris a une population très importante, alors que des villes plus petites comme “Bez et esparon” n’apparaîtront qu’à quelques reprises (population < 2000 personnes), parce que la population y est très faible. Un emprunteur est plus susceptible de vivre à Paris, car la population y est beaucoup plus importante.
En fait, les variables catégorielles contiennent souvent quelques étiquettes dominantes qui représentent la majorité des observations et un grand nombre d’étiquettes qui n’apparaissent que rarement.
Les étiquettes rares dans une variable catégorielle posent-elles un problème ?
Les valeurs rares peuvent ajouter beaucoup d’informations, voire aucune. Prenons par exemple une assemblée d’actionnaires où chaque personne peut voter proportionnellement au nombre de ses actions. L’un des actionnaires possède 50 % des actions, et les 999 autres actionnaires possèdent les 50 % restants. Le résultat du vote est largement influencé par l’actionnaire qui détient la majorité des actions. Les autres actionnaires peuvent avoir un impact collectif, mais ils n’ont pratiquement aucun impact individuel.
La même chose se produit dans les ensembles de données de la vie réelle. L’étiquette qui est surreprésentée dans l’ensemble de données a tendance à dominer le résultat, et ceux qui sont sous-représentés peuvent n’avoir aucun impact individuellement, mais pourraient avoir un impact s’ils sont considérés collectivement.
Plus précisément,
Les valeurs rares des variables catégorielles ont tendance à provoquer un surajustement, en particulier dans les méthodes basées sur les arbres.
Un grand nombre d’étiquettes peu fréquentes ajoutent du bruit, avec peu d’informations, provoquant ainsi un sur-ajustement.
Des étiquettes rares peuvent être présentes dans la série d’entraînement, mais pas dans la série de test, ce qui entraîne un surdimensionnement de la série d’entraînement.
Des étiquettes rares peuvent être présentes dans l’ensemble de test, mais pas dans l’ensemble d’entrainement. Ainsi, le modèle d’apprentissage en machine ne saura pas comment l’évaluer.
Note Des valeurs parfois rares, sont en effet importantes. Par exemple, si nous construisons un modèle pour prédire les demandes de prêts frauduleux, qui sont par nature rares, alors une valeur rare dans une certaine variable, peut en effet être très prédictive. Cette valeur rare pourrait nous indiquer que l’observation est très probablement une demande frauduleuse, et nous choisirions donc de ne pas l’ignorer.
Dans ce notebook :
Nous allons essayer:
- Apprendre à identifier les étiquettes rares dans un ensemble de données
- Comprendre combien il est difficile d’en tirer des informations fiables.
- Visualiser la répartition inégale des étiquettes rares entre les trains et les bancs d’essai
Je dis essayer car je ne sais pas du tout si nous avons des étiquettes rares.
La variable jockey montre 1943 états différents.
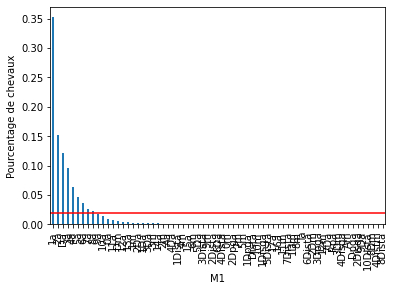
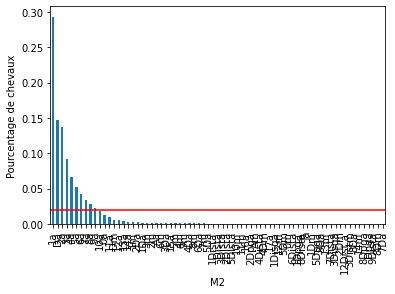
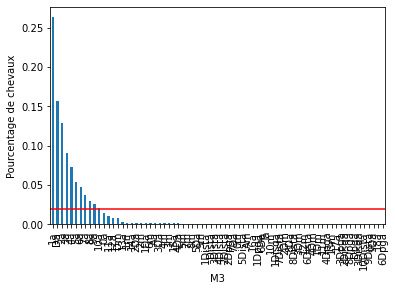
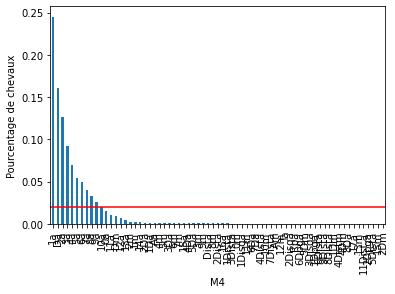
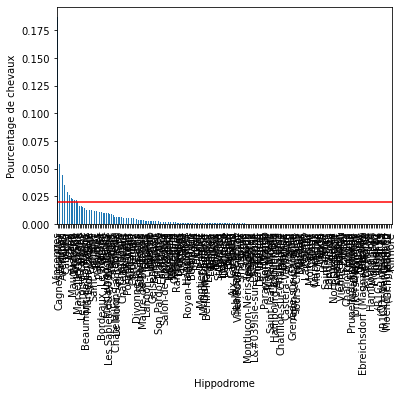
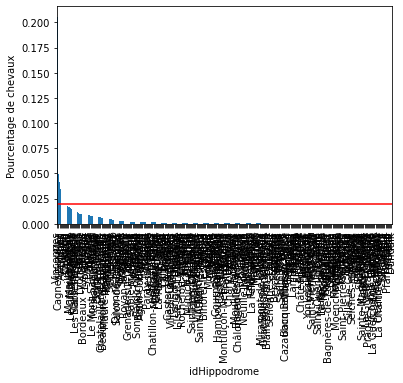
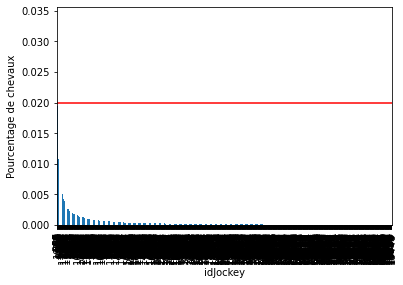
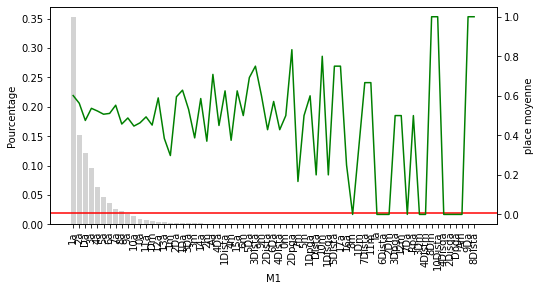
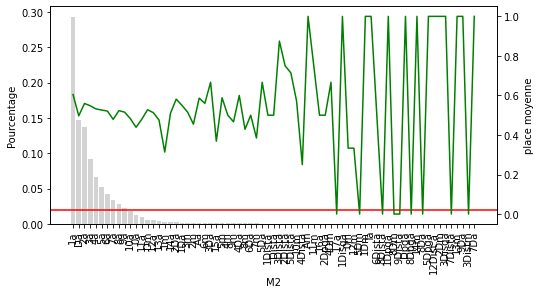
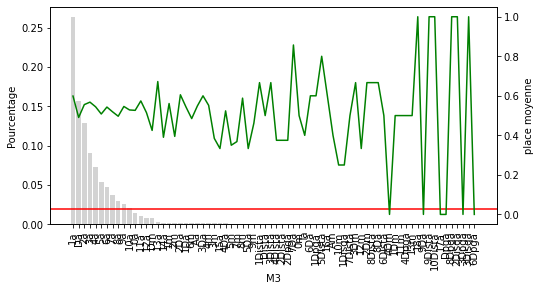
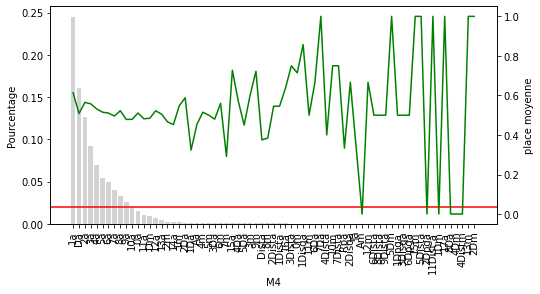
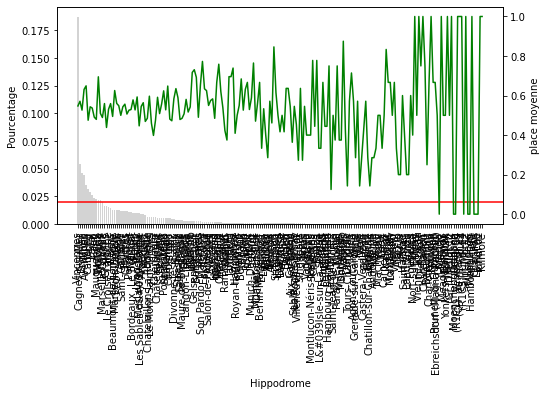
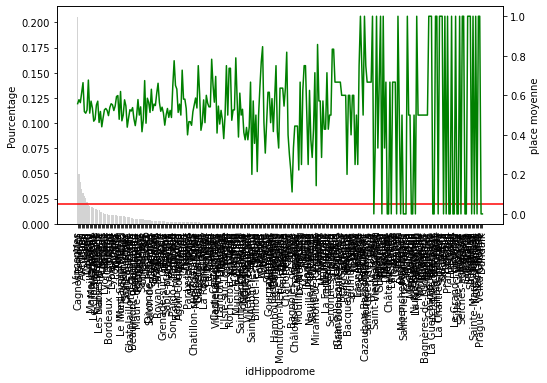
Pour chacune des variables catégorielles, certains labels apparaissent dans plus de 10 % des chevaux et beaucoup apparaissent dans moins de 10 % ou même 5 % des chevaux. Il s’agit d’étiquettes peu fréquentes ou de valeurs rares qui pourraient entraîner un sur-ajustement.
Quel est le rapport entre l’objectif “Place” et ces catégories ?
Dans les cellules suivantes, je veux comprendre la place à l’arrivée en fonction de l’étiquettes. Pour rappel, place vaut 1 quand le cheval est dans les 3 premiers et 0 dans les autres cas.
Continuez à lire, cela deviendra plus clair.
Le cadre de données ci-dessus contient le pourcentage de chevaux qui affichent chacune des étiquettes du jockey.
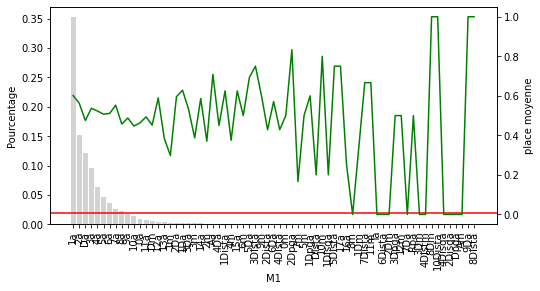
Ce que nous pouvons voir sur ce graphique c’est que plus la place à l’arrivée décroit en fonction de la position du cheval à l’arrivée dans sa dernière course. Je sais j’enfonce une porte ouverte mais cela est utile à visualiser. Par contre on ne peut rien tirer comme infos supplémentaires utilisables.
Étiquettes rares : regroupement sous une nouvelle étiquette
Une façon courante de travailler avec des valeurs rares ou peu fréquentes est de les regrouper sous une catégorie appelée “Rare” ou “Autre”. De cette façon, nous sommes en mesure de comprendre l’effet “collectif” des étiquettes peu fréquentes sur la cible.
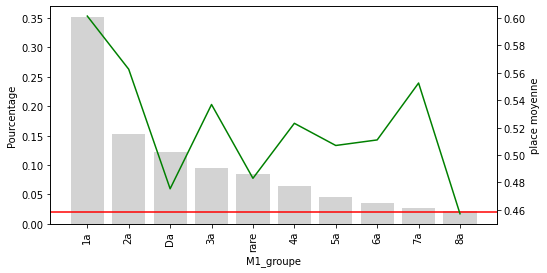
“Rare” contient maintenant l’influence globale de toutes les catégories peu fréquentes sur la place.
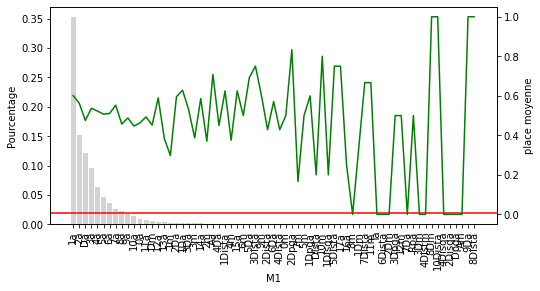
Seules 10 catégories de M1 sont relativement courantes dans l’ensemble des données. Les autres sont maintenant regroupées dans la catégorie “rare”. On voit clairement que la cétagorie rare est positionnée nettement moisn bien que les autres catégories
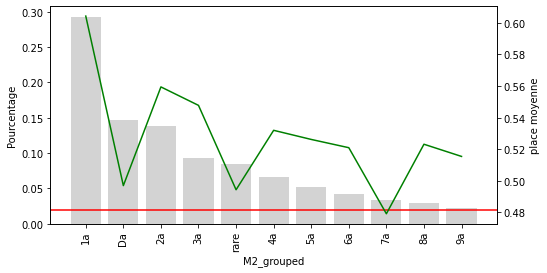
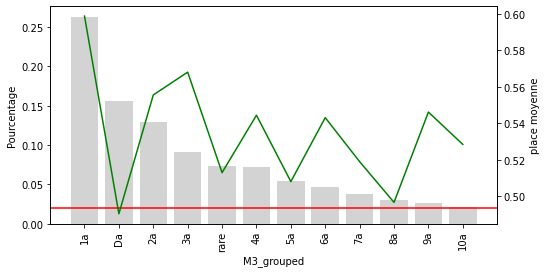
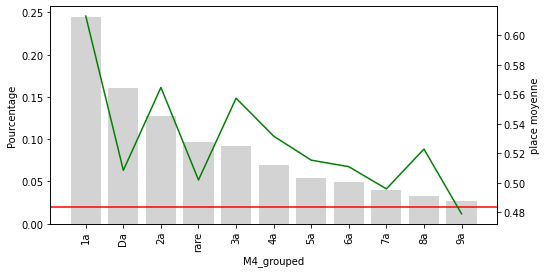
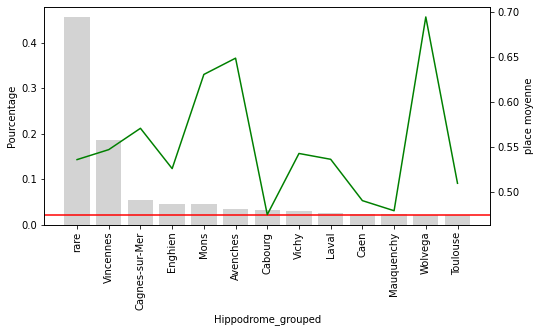
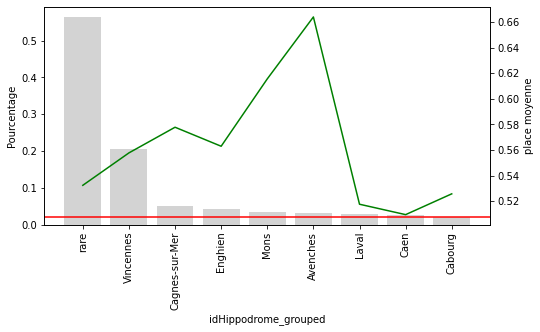
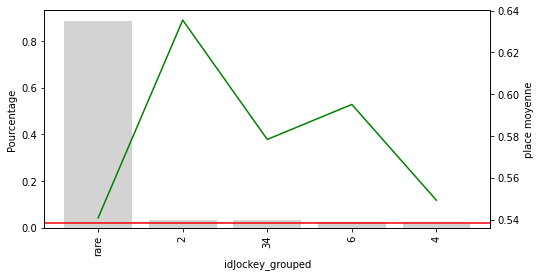
Pour les M2 à M4 on peut voir clairement que la catégorie rare sous performe nettement. Pour les hippodromes et le jockey, la catégorie rare avec un seuil de 2% ne semble pas adaptée.
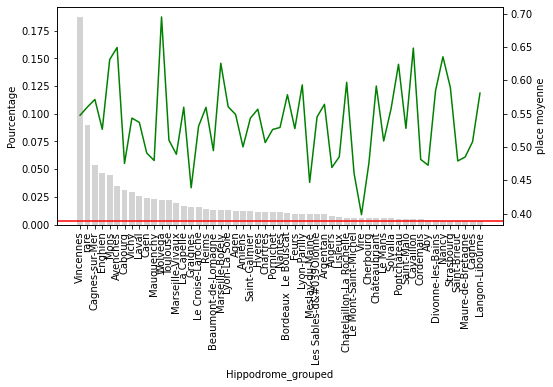
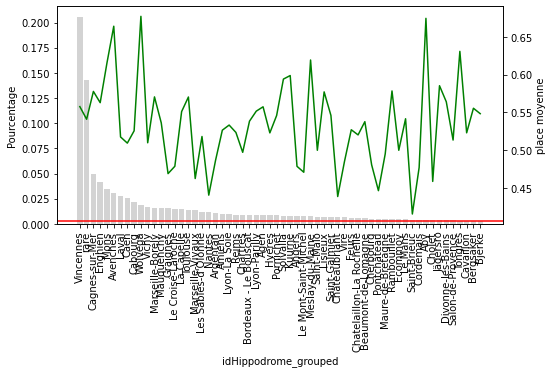
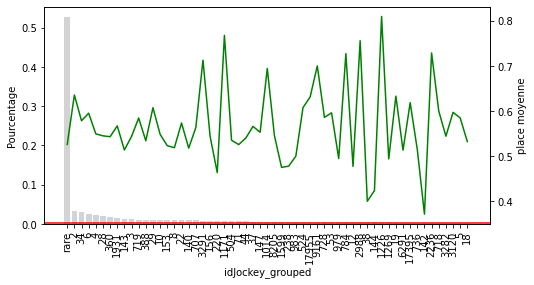
Il y a vraiment des hippodromes et des jockeys qui ont une “mauvaise” influence sur le résultat des chevaux.
