Une valeur aberrante est un point de données qui est significativement différent des autres données. “Une observation aberrante est une observation qui s’écarte tellement des autres observations qu’elle éveille des soupçons quant au fait qu’elle a été générée par un mécanisme différent”.
Faut-il supprimer les observations aberrantes ?
Selon le contexte, les observations aberrantes méritent une attention particulière ou doivent être complètement ignorées. Prenons l’exemple de la prévision des revenus : si des pics de revenus inhabituels sont observés, il est probablement bon d’y accorder une attention particulière et de déterminer la cause de ces pics. De la même manière, une transaction inhabituelle sur une carte de crédit est généralement le signe d’une activité frauduleuse, ce que l’émetteur de la carte de crédit veut empêcher. Dans de tels cas, il est donc utile de rechercher et d’examiner plus avant les valeurs aberrantes.
Toutefois, si des valeurs aberrantes sont introduites en raison d’une erreur mécanique, d’une erreur de mesure ou de toute autre chose qui ne peut être généralisée, il est judicieux de supprimer ces valeurs aberrantes avant d’alimenter l’algorithme de modélisation avec les données. Pourquoi ? Parce que certains algorithmes sont sensibles aux valeurs aberrantes.
Quels modèles d’apprentissage machine sont sensibles aux valeurs aberrantes ?
Certains modèles d’apprentissage machine sont plus sensibles aux valeurs aberrantes que d’autres. Par exemple, AdaBoost peut traiter les valeurs aberrantes comme des cas “difficiles” et accorder un poids énorme aux valeurs aberrantes, produisant ainsi un modèle avec une mauvaise généralisation.
Les modèles linéaires, en particulier la régression linéaire, peuvent également être sensibles aux valeurs aberrantes.
Les arbres de décision ont tendance à ignorer la présence de valeurs aberrantes lorsqu’ils créent les branches de leurs arbres. En général, les arbres prennent des décisions en demandant si la variable x >= une certaine valeur, et donc l’aberration tombera de chaque côté de la branche, mais elle sera traitée de la même manière que les valeurs restantes, quelle que soit son importance.
Un article de recherche récent suggère que les réseaux neuronaux pourraient également être sensibles aux valeurs aberrantes, à condition que le nombre de valeurs aberrantes soit élevé et que l’écart soit également important. Je dirais que si le nombre de valeurs aberrantes est élevé (>15% comme le suggère l’article), alors il ne s’agit plus de valeurs aberrantes, mais plutôt d’une représentation équitable de cette variable.
Comment identifier les valeurs aberrantes ?
L’analyse des valeurs aberrantes et la détection des anomalies constituent un vaste champ de recherche consacré à l’optimisation des méthodes et à la création de nouveaux algorithmes permettant d’identifier de manière fiable les valeurs aberrantes. Il existe un très grand nombre de méthodes optimisées pour détecter les valeurs aberrantes dans différentes situations. Ces méthodes sont principalement destinées à identifier les valeurs aberrantes lorsque ce sont les observations sur lesquelles nous voulons effectivement nous concentrer, par exemple pour les activités frauduleuses liées aux cartes de crédit.
Je me concentrerai sur l’identification des valeurs aberrantes introduites par une erreur mécanique ou de mesure. Ces valeurs aberrantes qui sont en effet un cas rare dans la population, et qui pourraient être ignorées. Je montrerai comment identifier ces valeurs aberrantes, afin que dans les sections ultérieures du cours, nous puissions apprendre à les prétraiter avant d’utiliser la variable pour former les algorithmes d’apprentissage automatique.
Analyse des valeurs extrêmes
La forme la plus élémentaire de détection des valeurs aberrantes est l’analyse des valeurs extrêmes des données unidimensionnelles. La clé de cette méthode consiste à déterminer les queues statistiques de la distribution sous-jacente de la variable, puis à trouver les valeurs qui se situent à l’extrémité de ces queues.
Si la variable est normalement distribuée (gaussienne), alors les valeurs qui se situent en dehors de la moyenne plus ou moins 3 fois l’écart-type de la variable sont considérées comme des valeurs aberrantes.
- valeurs aberrantes = moyenne +/- 3* std
Si la variable est distribuée de façon asymétrique, une approche générale consiste à calculer les quantiles, puis la fourchette interquantile (IQR), comme suit :
- IQR = 75e quantile – 25e quantile
Une valeur aberrante se situera en dehors des limites supérieures et inférieures suivantes :
Limite supérieure = 75e quantile + (IQR * 1,5)
Limite inférieure = 25e quantile – (IQR * 1,5)
ou pour les cas extrêmes :
Limite supérieure = 75e quantile + (IQR * 3)
Limite inférieure = 25e quantile – (IQR * 3)
Identifier la distribution des variables
Dans les variables normalement distribuées, les valeurs aberrantes sont celles qui se situent au-delà de la moyenne plus ou moins 3 fois l’écart-type. Cependant, si les variables sont faussées, nous trouvons des valeurs aberrantes en utilisant la plage interquantile. Afin de décider de la méthode à utiliser pour détecter les valeurs aberrantes, nous devons d’abord connaître la distribution de la variable.
Nous pouvons utiliser des histogrammes et des graphiques Q-Q pour déterminer si la variable est normalement distribuée. Nous pouvons également utiliser des boxplots pour visualiser directement les valeurs aberrantes. Les boxplots sont un moyen standard d’afficher la distribution d’une variable en utilisant le premier quartile, la médiane, le troisième quartile et les moustaches.
En regardant un boxplot, vous pouvez facilement l’identifier :
- La médiane, indiquée par la ligne à l’intérieur de l’encadré.
- La fourchette interquantile (IQR), la boîte elle-même.
- Les quantiles, le 25e (Q1) est l’extrémité inférieure et le 75e (Q3) l’extrémité supérieure de la boîte.
- Les moustaches, qui s’étendent jusqu’à :
- la moustache supérieure : Q3 + 1,5 x IQR
- moustache inférieure : Q1 -1,5 x IQR
Toute valeur se situant en dehors des moustaches est considérée comme une valeur aberrante. Examinons les exemples ci-dessous.
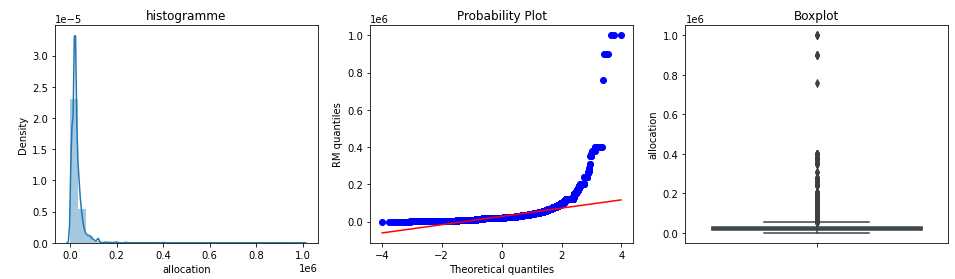
L’allocation n’est pas normalement distribuée. Elle est inclinée avec une queue vers la droite. Selon le boxplot, il y a quelques valeurs aberrantes à l’extrémité droite de la distribution de la variable.
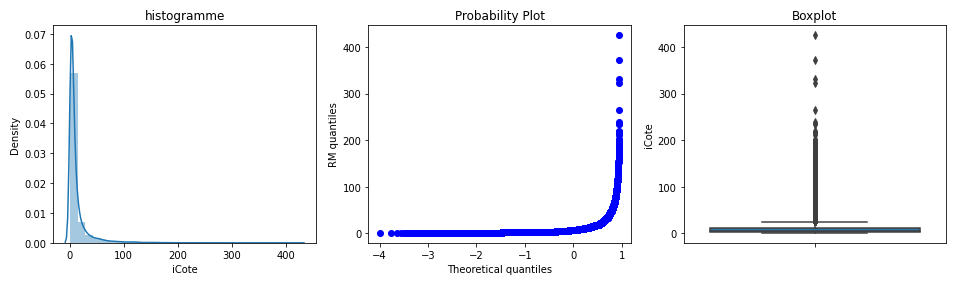
La cote n’est pas normalement distribuée. Elle est inclinée avec une queue vers la droite. Selon le boxplot, il y a quelques valeurs aberrantes à l’extrémité droite de la distribution de la variable.
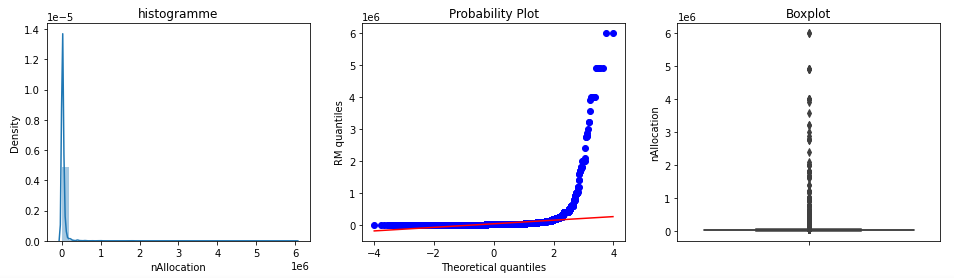
L’allocation de la dernière course n’est pas normalement distribuée. Elle est inclinée avec une queue vers la droite. Selon le boxplot, il y a quelques valeurs aberrantes à l’extrémité droite de la distribution de la variable.
Détection des valeurs aberrantes pour les variables biaisées
La limite supérieure indique une valeur de ~25.5. La limite inférieure est négative, mais la variable cote ne prend pas de valeur négative. Pour calculer les valeurs aberrantes de la cote, nous n’utilisons donc que la limite supérieure. Cela coïncide avec ce que nous avons observé dans le boxplot plus tôt dans le cahier. Les valeurs aberrantes se situent uniquement à la queue droite de la distribution de la cote.
Nous observons 1979 cas, soit 9,6 % de l’ensemble de données, avec des valeurs extrêmement élevées pour la cote.
En utilisant la fourchette interquantile de trois fois pour trouver des valeurs aberrantes, nous constatons qu’environ 6 % des cotes présentent des zones exceptionnellement élevées.
Toutes les variables de nos données présentent une queue à droite, la limite inférieure est négative. Nous utiliserons donc la limite supérieure pour déterminer les valeurs aberrantes. Nous observons que 6 % des valeurs de l’ensemble de données se situent au-dessus de la limite.

Je télécharge mon guide gratuit
Thank you!
You have successfully joined our subscriber list.
Vous recevrez votre guide par email sans aucun engagement de votre part.